今回はアルゴリズムとCPUのパワーでパズルを全力で解きます。
Exponential Idle（Android版 / iOS版）というクリッカー系放置ゲーム中のミニゲームである、矢印パズルを攻略します。
こちらのnoteの記事にめっちゃ影響を受けて書くことにしました。
と言っても、初級と中級は私でも頑張れば解けたのと、上級も先行研究があるので、エキスパートに絞って話を進めていきます（まあ上級も同じプログラムをちょちょっといじれば簡単に解けますが）。

訂正とお詫び

前回のサムネイルの一部に「♪ラデツキー行進曲（1.5倍速）」とありましたが、正しくは1.543倍速です。謹んでお詫び申し上げます。

ルール説明（エキスパート）

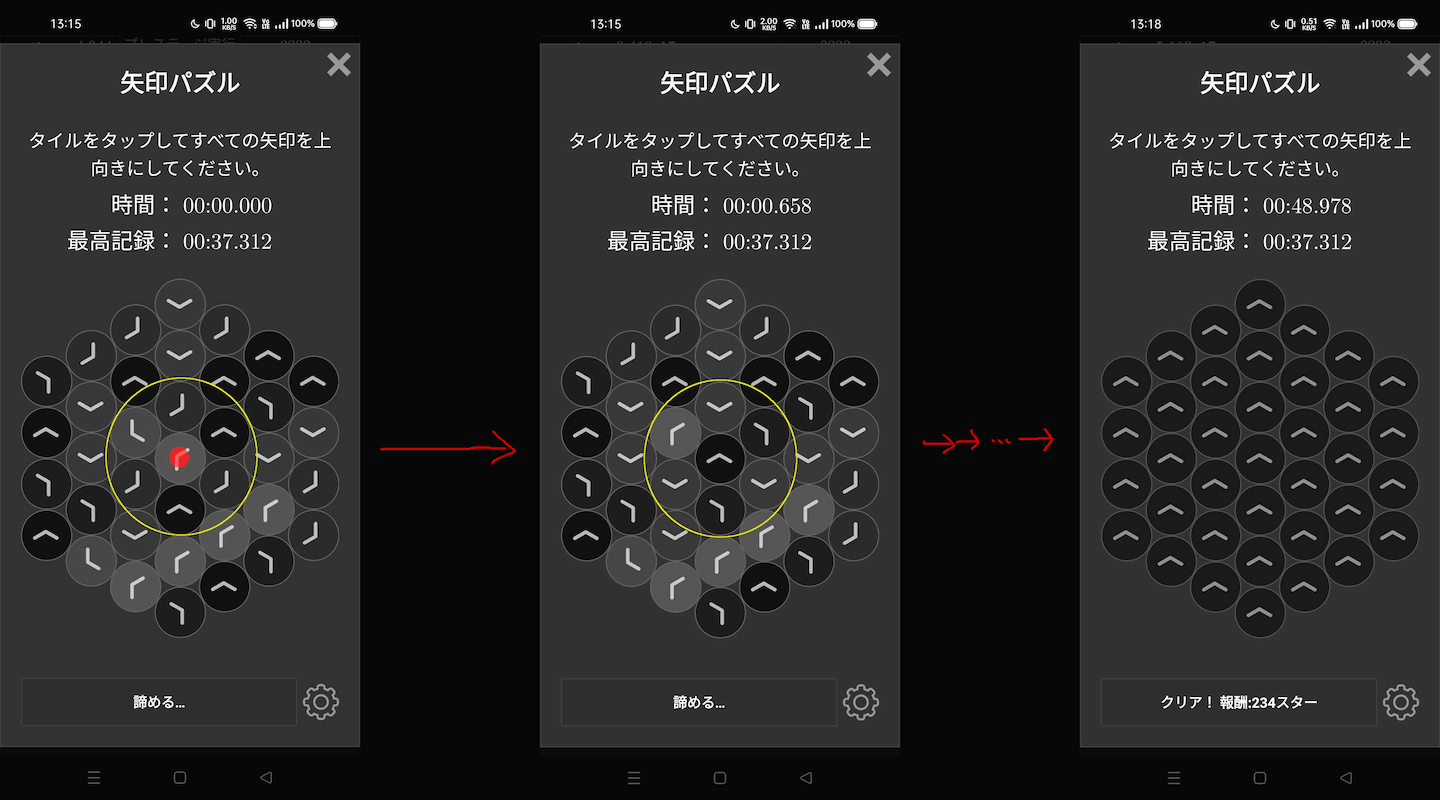
図1：矢印パズル（エキスパート）のルール

六角格子状に並べられたタイルをタップすると、そのタイルを含む周囲（最大）7個のタイルがそれぞれ時計回りに60°回転します。
それを繰り返してすべてのタイルの向きを上向きに揃える、というルールです。

目標

盤面を入力として受け取り、各タイルのタップ回数を出力する。

基本の考え方

1回タップすることに60°回転するので、6回同じ場所をタップすれば盤面の状態は変わらず、加法巡回群をなすような6元集合、$\mathbb{Z}/6\mathbb{Z}$ を持ってくる。

解法案

1

参考文献[3]と同様に、$\mathbb{Z}/6\mathbb{Z}$ 上の37次の線形方程式を解くことに帰着させる方法です。が。
聡明な読者の方ならお気づきでしょう。$\mathbb{Z}/6\mathbb{Z}$ は体でしょうか。2,3,4は乗法逆元を持たないので体ではないですね。
すると線形方程式を解くときに除法が使えないということになり、掃き出し法は使えないことになります（ピボットを1にできないだけで掃き出せないわけではないだろうが、一般的なアルゴリズムをそのまま持ってくるのは厳しそう）。

2

掃き出しで解けない（難しい）と言っても、元は有限個しかないので $6^{37}=6.2 \times 10^{28}$ 通りすべてを試してしまえという考え方。猿。
いや無理やけど。もし1パターンを1nsで検証できたとしても6.2e19 s掛かります。実際は1パターンの検証で約7x37回の足し算をすることになるのでもっとかかります。
imos法で最適化すればどうにかなるようなレベルの話ではないです。やるだけ無駄。

3

大本命。DFSです。DFS自体は木の全探索なのですが、探索の必要がない部分を枝刈りすればだいぶ計算量が減ります。どれぐらい絞れるかは後述。
今回はこれを採用。

プログラム

これが解を探索するプログラムです。
入力の数字は、ディスプレイモードを数字にして表示された数字ということになっています（内部的には-1して持っているが）。

#include <iostream>
#include <vector>
#include <tuple>
#include <algorithm>

using index_t = std::tuple<int, int>;
using board_t = std::vector<std::vector<int>>;

const int mod = 6;
const size_t board_row = 7, board_col = 7;

void dfs(board_t &board, board_t &hands, index_t index);
void flip_around(board_t &board, index_t index, int amount);
index_t next(index_t index);
bool is_in_board(index_t index);
void print_board(const board_t board);

const index_t end_index = next({ 6, 6 });

int main() {
  board_t board(board_row, std::vector<int>(board_col));
  board_t hands(board_row, std::vector<int>(board_col));
  for (index_t i = { 0, 0 }; i != end_index; i = next(i)) {
    const auto [r, c] = i;
    std::cout << r << " " << c << ": " << std::flush;
    std::cin >> board[r][c];
    board[r][c]--;
  }
  dfs(board, hands, { 0, 0 });
  return 0;
}

void dfs(board_t &board, board_t &hands, index_t index) {
  if (index == end_index) {
    print_board(hands);
    exit(0);
    return;
  }
  auto [r, c] = index;
  // 右端辺での枝刈り
  if (c == 6 && r > 3 && board[r - 1][c - 1] != board[r - 1][c]) {
    return;
  }
  // 下端辺での枝刈り
  if (r == 6 && c > 3 && board[r - 1][c - 1] != board[r][c - 1]) {
    return;
  }
  // 上端、左端辺以外での枝刈り
  if (r != 0 && c != 0) {
    // 左上マスを0にするように動かす
    const int hand = (mod - board[r - 1][c - 1]) % mod;
    hands[r][c] = hand;
    flip_around(board, index, hand);
    dfs(board, hands, next(index));
    flip_around(board, index, mod - hand);
  } else {
    for (int hand = 0; hand < mod; hand++) {
      hands[r][c] = hand;
      flip_around(board, index, hand);
      dfs(board, hands, next(index));
      flip_around(board, index, mod - hand);
    }
  }
}

void flip_around(board_t &board, index_t index, int amount) {
  // 正体不明だがちゃんと最初だけ初期化処理が走る
  static std::array<index_t, 7u> dpos{
    dpos[0] = { -1, -1 },
    dpos[1] = { -1, 0 },
    dpos[2] = { 0, -1 },
    dpos[3] = { 0, 0 },
    dpos[4] = { 0, 1 },
    dpos[5] = { 1, 0 },
    dpos[6] = { 1, 1 }
  };
  const auto [r, c] = index;
  for (const auto [dr, dc] : dpos) {
    if (!is_in_board({ r + dr, c + dc })) continue;
    board[r + dr][c + dc] += amount;
    board[r + dr][c + dc] %= mod;
  }
}

index_t next(index_t index) {
  auto [r, c] = index;
  if (c == 6 || c - r >= 3) {
    r++;
    c = std::max(r - 3, 0);
  } else {
    c++;
  }
  return { r, c };
}

bool is_in_board(index_t index) {
  auto [r, c] = index;
  return std::abs(r - 3) <= 3 && std::abs(c - 3) <= 3 && std::abs(c - r) <= 3;
}

void print_board(const board_t board) {
  for (size_t i = 0; i < board_row; i++) {
    for (size_t j = 0; j < board_col; j++) {
      if (is_in_board({ i, j })) {
        std::cout << board[i][j] << " ";
      } else {
        std::cout << "  ";
      }
    }
    std::cout << "\n";
  }
  std::cout << std::endl;
}

こんなに const とか & とか書くんだったら最初からRustでやればよかったなと若干の後悔。
ぼちぼち解説していきます。

まずここ。

using index_t = std::tuple<int, int>;
using board_t = std::vector<std::vector<int>>;

index_t というエイリアスに std::tuple<int, int> を当てています。
index_t index = {row, column}; となっているならば、index は、row 行 column 列のパネルの位置を表します。
board_t には std::vector<std::vector<int>> を当てていますが、
board_t board(R, std::vector<int>(C)); としたならば、board は、R 行 C 列のパネルの二次元配列を表します。（入力と）パネルの現状態と出力する手数に使います。

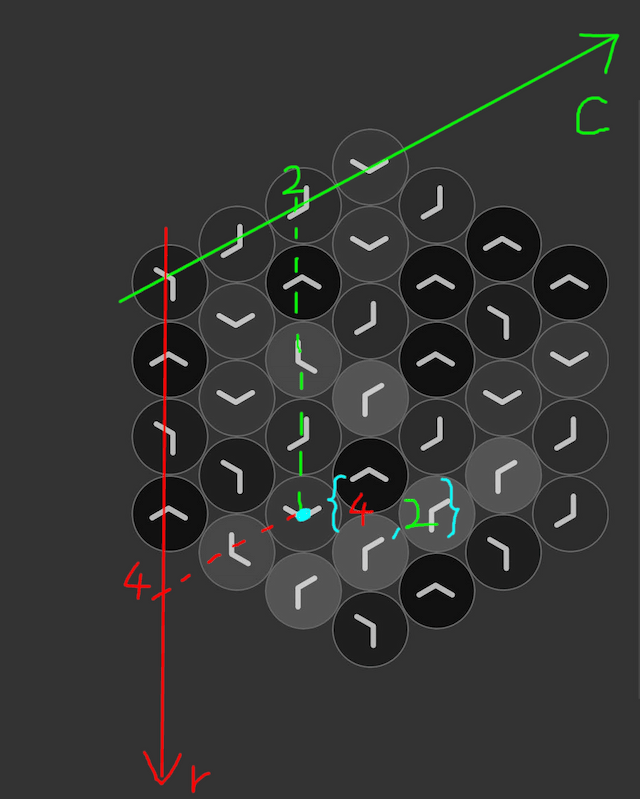
図2：indexの指し方

次はここ。

index_t next(index_t index) {
  auto [r, c] = index;
  if (c == 6 || c - r >= 3) {
    r++;
    c = std::max(r - 3, 0);
  } else {
    c++;
  }
  return { r, c };
}

next関数はその名の通り、次に探索する（タップ回数を決定する）点を決定する関数で、DFSでの探索順に直接関わってきます。
定義はまあ見りゃわかりますね（ifの条件に c - r >= 3 とか書いてあるが、これは条件をいっぱい書きたくなかったからうまいこと纏めてあるだけ）。
2行目の auto [r, c] = index; ってのは構造化束縛というC++17以降で追加された機能です。分割代入だと思って大体問題ありません。
一応探索順を図に示しておくとこうです。

図3：DFSの探索順

この順序にしているのは、単純に分かりやすいという以外にもう一点理由があって、枝刈りがしやすいという点。
枝刈りの方法はdfs関数を見ればわかります。

void dfs(board_t &board, board_t &hands, index_t index) {
  if (index == end_index) {
    print_board(hands);
    exit(0);
    return;
  }
  auto [r, c] = index;
  // 右端辺での枝刈り
  if (c == 6 && r > 3 && board[r - 1][c - 1] != board[r - 1][c]) {
    return;
  }
  // 下端辺での枝刈り
  if (r == 6 && c > 3 && board[r - 1][c - 1] != board[r][c - 1]) {
    return;
  }
  // 上端、左端辺以外での枝刈り
  if (r != 0 && c != 0) {
    // 左上マスを0にするように動かす
    const int hand = (mod - board[r - 1][c - 1]) % mod;
    hands[r][c] = hand;
    flip_around(board, index, hand);
    dfs(board, hands, next(index));
    flip_around(board, index, mod - hand);
  } else {
    for (int hand = 0; hand < mod; hand++) {
      hands[r][c] = hand;
      flip_around(board, index, hand);
      dfs(board, hands, next(index));
      flip_around(board, index, mod - hand);
    }
  }
}

私もそこまでアホではないし、この関数は深い再帰を伴うので引数の大部分は参照で受けるようにしました。
部のC#erの皆さんが卒倒するかもしれませんが、vector<T>は値型です。というか、C/C++に値型・参照型という分け方はありません。
明示しない限り常にすべて値渡しになるので、ちゃんと参照渡しになるよう指定してやります。

さておき、枝刈りの話。これも図に示したほうが早いでしょう。

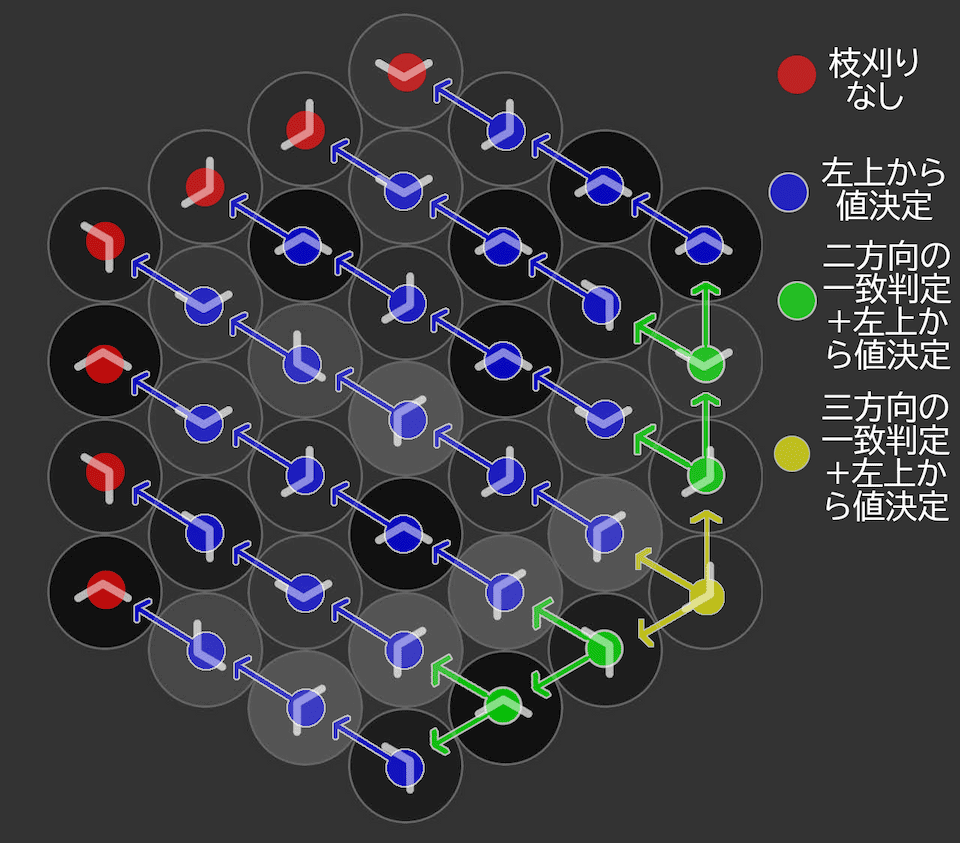
図4：dfs関数の枝刈り

図3に示した探索順から分かるように、27,32,36のノードでは、そのノードを操作した後は左上と真上の変化がないので、その2箇所の状態は必ず同じでなければならず、そうでなければ後退して探索し直すことになります。34,35,36でも左上と左下で同じことが起こります。
また図3から分かるように、ある時点で探索しているパネルの左上にパネルがあったとき、探索しているパネルを動かした後に再び左上のパネルが変わることはないので、左上は0にならなくてはなりません。よって左上のパネルを元にただ一通りに決まります。逆に言えば、0～5の中から自由に選べるのは左上にパネルが存在しない0,1,2,3,4,9,15のたった7個のパネルのタップ回数のみです。したがって、検証の必要なパターン数は $6^7 \approx 10^{5.45}$ 通りだけになります（ただし、関数呼び出し自体が重いことと、これらの点の不正性が分かるまでに再帰の深いところに潜ることがあるのでやはりある程度計算に時間はかかる）。
こんな感じで殆どの点で枝刈りが行えることがわかりますね。

if (index == end_index) {
  print_board(hands);
  exit(0);
  return;
}

で、最後36番が終わればここの分岐にたどり着いて終わりです（なんでこの人exitとreturn両方書いてるんだろう）。
でも図4を見てもらえばわかりますが、36番ノードだけチェックが入ってないんですよね。
これでいいのかと言われれば良くて、解が存在するならば、36番ノードだけが非0であることはありません。
流石に解が存在しない問題は生成されないだろうということでここは一つ。

flip_around(board, index, hand);
dfs(board, hands, next(index));
flip_around(board, index, mod - hand);

ところでこの部分ですが、再帰DFSにおける常套手段です。
ある変換（ここではある1パネルをn回タップすること）が可逆であるならば、dfs呼び出しから帰ってきた後に逆変換（ここでは同じパネルを6-n回タップすること）を行えばうまいことDFSになります。是非覚えておいてください。

以上。

閑話

void flip_around(board_t &board, index_t index, int amount) {
  // 正体不明だがちゃんと最初だけ初期化処理が走る
  static std::array<index_t, 7u> dpos{
    dpos[0] = { -1, -1 },
    dpos[1] = { -1, 0 },
    dpos[2] = { 0, -1 },
    dpos[3] = { 0, 0 },
    dpos[4] = { 0, 1 },
    dpos[5] = { 1, 0 },
    dpos[6] = { 1, 1 }
  };
  ...
}

この部分、何ですか。自分で書いたけどどういう理屈で初期化されているのかわかりません。C++プロの方、教えて下さい。
aggregateならメンバ名を指定して初期化する方法があるけど、その延長と考えていいんですかね。

参考文献

[1]Conic Games「Exponential Idle - Google Play のアプリ」<https://play.google.com/store/apps/details?id=com.conicgames.exponentialidle>
[2]Gilles-Philippe Paille「「Exponential Idle」をApp Storeで」<https://apps.apple.com/jp/app/exponential-idle/id1538487382>
[3]ちゃそ「Exponential Idle #2 矢印パズル攻略法（と二元体GF(2)上の線形方程式について）」<https://note.com/so_ra_64/n/n9c2eb6a5ef6f>
[4]ますたー。/繰り上げP「焼き甜花ちゃんシリーズの作り方＆素材」<https://www.nicovideo.jp/watch/sm37861810>
[5]いもす研「いもす法」<https://imoz.jp/algorithms/imos_method.html>