はじめに

こんにちは、ごまです！
つい最近、Python で微分方程式を解いたり、グラフを描画することを可能にするライブラリがあることを知りました。
自分の知る限りでは、微分方程式を解くためには SymPy というライブラリが有効なようなのですが、正直なところあまり使ったことがありません。
そのため、SymPyの使い方を習得するためにも、今回はこのライブラリと Python を用いて、高校物理の問題を、それも (高校物理では殆どの場合考慮されなかった) 空気抵抗の考慮をしつつ解いてみようと思います。

環境

• Windows 11
• Python 3.9.7
• SymPy 1.11.1

SymPyについて軽く説明と実演

本格的に演習に入る前に、SymPyについての軽い説明と、いくつかの実演を行います。

今回使用するライブラリであるSymPyは、簡単に言うと数式の処理や計算を行えるPythonのライブラリです。
これを用いることで、Pythonを用いての微分積分や因数分解などの様々な数式の処理が可能になります。

前置きはここまでとして、実際にSymPyを使ってみます。本稿ではこれ以降、SymPyをsymとしてimportします。

import sympy as sym

因数分解

まずは因数分解をやってみましょう。
SymPyで$x$や $y$ などの変数を扱う際は、次のようにsympy.symbols()を用いて定義を行います。

x,y = sym.symbols('x,y')

もちろん1文字ずつ定義を行うことも可能です。

因数分解はsympy.factor()の引数として、因数分解したい数式を渡すことによって行えます。
今回は $2x^{4}-9x^{3}-x^{2}-9x+2$という数式を因数分解してみます。
具体的には次のように記述します。

sym.factor(2*x**4 -9*x**3 -x**2 -9*x +2)

少し記法が分かりづらいですが、この場合の*(アスタリスク)一つは乗算演算子、二つはべき乗演算子です。
例えば $a \times b$ はa*b、 $a^{b}$ はa**bと表現されます。
因数分解の結果は次のようになりました。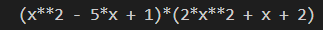

どうやら無事に因数分解できたようです。
これも記法が分かりづらいですが、SymPy はsympy.latex() を用いることで、数式を LaTeX の記法で出力してくれます。
そのため次のような関数 output() を定義することで、以降の結果を LaTeX の記法で出力することとします。

def output(ans):
    print("\n",sym.latex(ans),"\n")

実際に先程の計算を引数にして output() を実行すると次のような出力が得られました。
したがって結果は $ \left(x^{2} - 5 x + 1\right) \left(2 x^{2} + x + 2\right) $ となり、やはり問題なく因数分解できていることがわかります。

微分積分

微分積分についても扱っておきます。

まず微分ですが、sympy.diff()を用いることで導関数を求めることができます。
例えば、 $x^{3}$ の $x$ に関しての1階微分は次のように書くことができ、結果として $3x^{2}$ が出力されます。

output(sym.diff(x**3,x))

$n$ 回微分をしたければ、 $n$ の数だけ変数を渡すか、変数のあとに $n$ を渡すことによって行えます。
例えば、 $x^{3}$ の $x$ に関しての2階微分は次のように書くことができ、結果としてどちらも $6x$ が出力されます。

output(sym.diff(x**3,x,x))
output(sym.diff(x**3,x,2))

次に積分について説明します。不定積分を行う際はsym.integrate()関数に式と変数を与えればよいです。
例えば、 $6x$ を $x$ について不定積分しようとする場合は次のように書くことができ、結果として $3x^{2}$ が出力されます。

output(sym.integrate(6*x))

積分定数が含まれていませんが、これは微分方程式を解く場合には問題ありません。

定積分については、定積分の下限と上限を与えることで計算が行なえます。
次の計算では結果として48を得ます。

output(sym.integrate(6*x,(x,3,5)))

微分方程式

今回の記事で最も重要な、微分方程式の計算について説明します。
まず次のように、変数 $x$ に加えて、未定義の関数$f$を宣言します。
関数の宣言はsympy.Function()で行います。

x = sym.symbols('x')
f = sym.Function('f')

そして、関数 $f(x)$ についての微分方程式を次のように宣言します。
今回解く微分方程式は
$$\frac{d^{2}}{dx^{2}}f(x)-\frac{d}{dx}f(x)-2f(x)=0$$
です。

eq = sym.Eq(f(x).diff(x, x) - f(x).diff(x) - 2*f(x), 0)

方程式の定義はsympy.Eq()で行います。第一引数は方程式の左辺、第二引数は方程式の右辺です。
右辺は今回は0に設定していますが、勿論他の引数を渡すこともできます( $e^x$ とか)。

そして、微分方程式はsympy.dsolve()関数に先程宣言した方程式eqを引数として渡すことにより解くことができます。

output(sym.dsolve(eq, f(x)))

その結果、
$$f{\left(x \right)} = C{1} e^{- x} + C{2} e^{2 x} $$
が出力されました。
今回は不定積分のときと異なり、適切に任意定数 $C{1},C{2}$ が用いられています。
本稿ではこれを用いて、運動方程式の解を求めていきます。

今回扱う問題

今回は河合出版の「物理のエッセンス 四訂版 力学・波動」の中から、簡単な力学の問題を抜粋して解いていきます。
比較のため、それぞれの問題に対して「空気抵抗ナシ」「空気抵抗アリ」の両方のパターンの解答の流れを示します。

演習

放物運動

問題

質量$m$の質点を床から初速$v_{0}$で角度$\theta$の方向に投げた場合,

1. 最高点に達するまでの時間$t_{1}$と最高点の高さ$h$を求めよ。
2. 水平到達距離$x$を求めよ。

解答(空気抵抗ナシ)

1. 水平方向に $x$ 軸、鉛直方向に $y$ 軸を取ることを考えると、鉛直方向の運動方程式は
$$m\frac{d^{2}y}{dt^{2}}=-mg$$
となります。
両辺を $m$ で割り $g$ を移項すると
$$\frac{d^{2}y}{dt^{2}}+g=0$$
となるため、これをSymPyで記述すると

eq1_0 = sym.Eq(y(t).diff(t, 2)+g)

これを微分方程式としてsympy.dsolve()を用いて解く際、

eq1_2 = sym.dsolve(eq1_0, y(t))

と記述することができ、この解は
$$
  y{\left(t \right)} = C_{1} + C_{2} t - \frac{g t^{2}}{2}
$$
となリます。

実は、SymPyでは微分方程式を解く際に初期条件を課すことができ、ics={}の形で記述できます。
今回、 $y(0)=0$ 、 $\frac{dy}{dt}(0)=v_{0}\sin\theta$ ですから、先程の式は

eq1_2 = sym.dsolve(eq1_0, y(t), ics={y(0): 0, y(t).diff(t, 1).subs(t, 0): v0*sym.sin(theta)})

と書き直すことができます。subs()関数は代入を行っていると考えていただければ大丈夫です。
$y(t)$ の１階微分に $t=0$ を代入したとき、その値が $v_{0}\sin\theta$ であるということを表しています( $v_{0}$ と $\theta$ は新たにsympy.symbolsで定義しました)。
そうして改めて微分方程式を解くと、解として
$$
  y{\left(t \right)} = - \frac{g t^{2}}{2} + t v_{0} \sin{\left(\theta \right)}
$$

が得られます。
したがって、これの両辺を $t$ について微分した式は
$$
\frac{dy}{dt}=-gt+v_{0}\sin\theta
$$
ですから、 $t=t_{1}$ のとき、すなわち最高点における $y$ 方向の速さが0であることから、この式の左辺を0とおいた式を$t$ について次のように解きます。

t_1 = sym.solve(eq1_1, t)

これによって、解が次のように出力されます。


したがって、
$$
  t_{1}= \left[ \frac{v_{0} \sin{\left(\theta \right)}}{g}\right]
$$

ということがわかります。

最高点 $h$ を求めるには、この $t_1$ を(4)式に代入すればいいわけですから、

h = eq1_2.subs(t, ((v0*sym.sin(theta)/g)))

このように記述してやることで、値として
$$
  y{\left(\frac{v_{0} \sin{\left(\theta \right)}}{g} \right)} = \frac{v_{0}^{2} \sin^{2}{\left(\theta \right)}}{2 g}
$$
が得られます。これが$h$ですから、書き直すと
$$
h = \frac{v_{0}^{2} \sin^{2}{\left(\theta \right)}}{2 g}
$$
となり、少々不格好ですが無事に小問1が解けたことになります。

2.投げ出されてから落下するまでの時間を $t_{2}$ とすると$t=t_{2}$のとき$y=0$ですから、

t_2 = sym.solve(eq1_2.subs(y(t),0), t)

と記述してやることで、解として
$$
\left[ 0, \ \frac{2 v_{0} \sin{\left(\theta \right)}}{g}\right]
$$
が得られます。$t_{2}\neq0$ですから、
$$
t_{2}=\frac{2 v_{0} \sin{\left(\theta \right)}}{g}(=2t_{1})
$$
であることは明らかです。

ここで、質点に対しては水平方向の力は何も加わっていませんから、水平方向の運動方程式は次のようになります。
$$
  m\frac{d^{2}x}{dt^{2}}=0
$$
したがって両辺を $m$ で割ったものをこのように記述します。

eq2_0=sym.Eq(x(t).diff(t, 2))

これを、微分方程式として、初期条件 $x(0)=0$ 、 $\frac{d}{dt}x(t)=v_{0}\cos\theta$ を課して解くには次のように記述すれば良く、

eq2_2 = sym.dsolve(eq2_0, x(t), ics={x(0): 0, x(t).diff(t, 1).subs(t, 0): v0*sym.cos(theta)})

解として
$$
x{\left(t \right)} = t v_{0} \cos{\left(\theta \right)}
$$

が得られます。
これに $t=t_{2}$ を代入して解くためには

x_l= eq2_2.subs(t, ((2*v0*sym.sin(theta)/g)))

と記述でき、解として
$$
  x{\left(\frac{2 v_{0} \sin{\left(\theta \right)}}{g} \right)} = \frac{2 v_{0}^{2} \sin{\left(\theta \right)} \cos{\left(\theta \right)}}{g}
$$
すなわち水平到達距離 $x$ として
$$
  x= \frac{2 v_{0}^{2} \sin{\left(\theta \right)} \cos{\left(\theta \right)}}{g}
$$
が得られます。

解答(空気抵抗アリ)

1. $x$ 軸および $y$ 軸を空気抵抗ナシの場合と同様に取ることを考えます。
ここで、空気抵抗の比例定数を $\kappa$ (カッパ)とすると、 $y$ 軸方向の運動方程式は次のようになります。
$$
  m\frac{d^{2}y}{dt^{2}}=-mg-\kappa\frac{dy}{dt}
$$
両辺を $m$ で割り移項すると
$$
  \frac{d^{2}y}{dt^{2}}+\frac{\kappa}{m}\frac{dy}{dt}+g=0
$$
となります。これを記述すると

eq1_0 = sym.Eq(y(t).diff(t, 2)+(kappa/m)*y(t).diff(t, 1)+g,0)

と書けますから、これを次のようにsympy.dsolve()を用いて、初期条件 $x(0)=0$ 、 $\frac{d}{dt}x(t)=v_{0}\cos\theta$ を課して解きます。

eq1_2 = sym.dsolve(eq1_0, y(t), ics={y(0): 0, y(t).diff(t, 1).subs(t, 0): v0*sym.sin(theta)})

すると次のような解が得られます。

$$
  y{\left(t \right)} = - \frac{g m t}{\kappa} + \frac{\left(- g m^{2} - \kappa m v_{0} \sin{\left(\theta \right)}\right) e^{- \frac{\kappa t}{m}}}{\kappa^{2}} + \frac{g m^{2} + \kappa m v_{0} \sin{\left(\theta \right)}}{\kappa^{2}}
$$
空気抵抗ナシの場合に比べて非常に式が複雑になっていますが、解法は特に変わりません。
式自体が長くなったので省略しましたが、式の両辺を微分すると
$$
\frac{d}{dt}y(t) = -\frac{g m}{\kappa} - \frac{\left(- g m^{2} - \kappa m v_{0} \sin{\left(\theta \right)}\right) e^{- \frac{\kappa t}{m}}}{\kappa m}
$$

となります。
あとは空気抵抗ナシの場合と同様に、 $t=t_{1} $のとき $dy/dt=0$ となると考えて、直前の式を用いて定義したeq1_1を $t$ について解くと、
sympy.solve()を用いて次のように書くことができ、

t_1 = sym.solve(eq1_1, t)

解として
$$
  t_{1}= \left[ \frac{m \log{\left(1 + \frac{\kappa v_{0} \sin{\left(\theta \right)}}{g m} \right)}}{\kappa}\right]
$$

が出力されます。最高点$h$も空気抵抗アリの場合と同様にして、 $t_1$ を $y(t)$ の式に代入すれば良く、

h = eq1_2.subs(t, m*sym.log(1 + kappa*v0*sym.sin(theta)/(g*m))/kappa)

と記述すれば、計算結果として
$$
y{\left(\frac{m \log{\left(1 + \frac{\kappa v_{0} \sin{\left(\theta \right)}}{g m} \right)}}{\kappa} \right)} = - \frac{g m^{2} \log{\left(1 + \frac{\kappa v_{0} \sin{\left(\theta \right)}}{g m} \right)}}{\kappa^{2}} + \frac{g m^{2} + \kappa m v_{0} \sin{\left(\theta \right)}}{\kappa^{2}} \\+ \frac{- g m^{2} - \kappa m v_{0} \sin{\left(\theta \right)}}{\kappa^{2} \cdot \left(1 + \frac{\kappa v_{0} \sin{\left(\theta \right)}}{g m}\right)}
$$
が得られますから、
$$
h= - \frac{g m^{2} \log{\left(1 + \frac{\kappa v{0} \sin{\left(\theta \right)}}{g m} \right)}}{\kappa^{2}} + \frac{g m^{2} + \kappa m v{0} \sin{\left(\theta \right)}}{\kappa^{2}} + \frac{- g m^{2} - \kappa m v_{0} \sin{\left(\theta \right)}}{\kappa^{2} \cdot \left(1 + \frac{\kappa v_{0} \sin{\left(\theta \right)}}{g m}\right)}
$$
とわかります。

2.こちらの問題も空気抵抗アリの場合と同様に解く、といいたいところですが、数式が複雑化してしまったせいか、
投げ上げてから落下するまでの時間を求める過程でプログラムが停止してしまい計算を完了することができませんでした。
そのため、残念ですがこのあたりは今後の課題とします。

余談

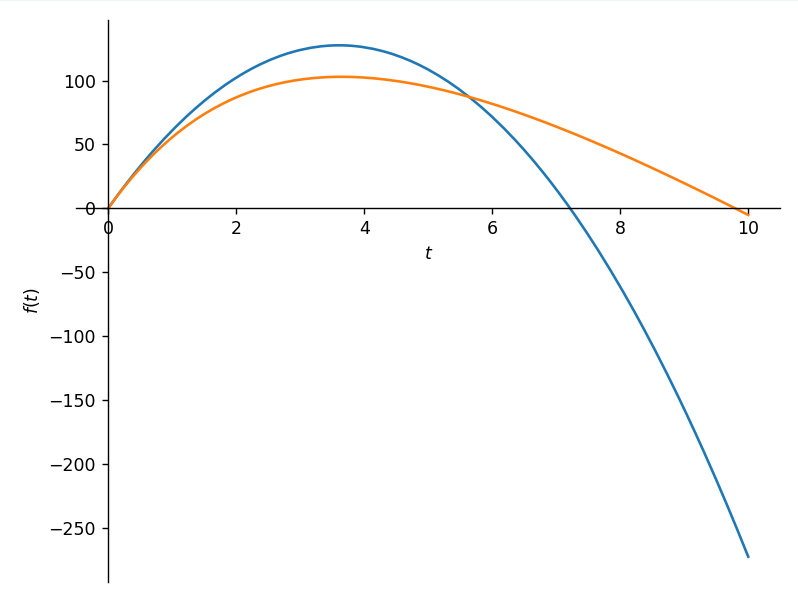
sympy.plot()を用いれば、物体が実際にどのような運動をするのか、というグラフをプロットすることができます。
次の図は私が適当に質点の質量やら投げる角度やら空気抵抗定数やらを指定してプロットした結果です。青が真空中での $y-t$ グラフ、オレンジが流体中での $y-t$ グラフです。

(ここで流体と表現したのは、空気抵抗定数あたりの計算を厳密にしなかったせいで現実ではありえない空気抵抗が発生している可能性があるからです。下手したらタイトル詐欺かも...)

終わりに

至らない点も多くありましたが、SymPyを用いた計算の方法を習得することができ、個人的には有意義な取り組みだったと思います。
もしかしたらまた同様の記事を書くかもしれません。ここまでご覧いただきありがとうございました。

参考文献

• maskot1977 . "微分や微分方程式をPythonで理解する" . "Qiita" . 2019-01-09 .https://qiita.com/maskot1977/items/b4395da5f33f70cd4a09, (参照 2023-02-20)
• 大窪 貴洋. "Sympyによる代数計算" . "コンピューター処理 ドキュメント" . 不明. https://amorphous.tf.chiba-.jp/lecture.files/chemcomputer/15Sympy%E3%81%AB%E3%82%88%E3%82%8B%E4%BB%A3%E6%95%B0%E8%A8%88%E7%AE%97/15.html,(参照 2023-02-27).
• SymPy Development Team. "SymPy". 2021. https://www.sympy.org/en/index.html, (参照 2023-02-28).
• 浜島清利, 物理のエッセンス四訂版　力学・波動, 河合出版, 2013