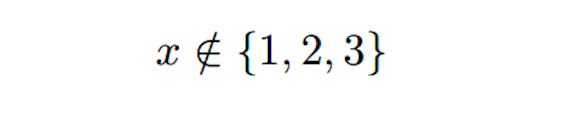はじめに

この記事はTypstシリーズの第5弾です。今回は趣向を変えて、大学の授業で扱う定理や法則を、Typstではどのように記述するかという点からTypstの記法を解説します。そのため前回の記事は読んでいなくても構いませんが、Typstの基本的な使い方については知っていることを前提としています。

前述の通り、今回は大学の授業で扱う定理や法則を取り上げます。私の専攻の関係上、扱う学問や定理に偏りがあるとは思いますが、記法自体は他の分野にも応用できるようになっているため、参考にしていただければ幸いです。また、今回は記法の紹介を行うのが主な目的のため、新しい記法を用いない定理や法則の紹介は行いません。

また、定理や法則の表示を整えるためにshowyboxというパッケージを使用しています。こちらの使い方には今回は触れませんが、興味がある方はぜひ試してみてください。

微分積分学

極限の基本性質

$lim_(n->oo) a_n=a$、$lim_(n->oo) b_n=b$とする。
#line(length: 100%)
$ lim_(n->oo) a_n plus.minus b_n=a plus.minus b $
#line(length: 100%)
$ lim_(n->oo) a_n  b_n=a  b $
特に、$k$が定数のとき
$ lim_(n->oo) k a_n = k a $
#line(length: 100%)
$ lim_(n->oo) a_n / b_n = a / b quad(b_n, b!=0) $
#line(length: 100%)
$a_n <= b_n$ならば$ a <= b $

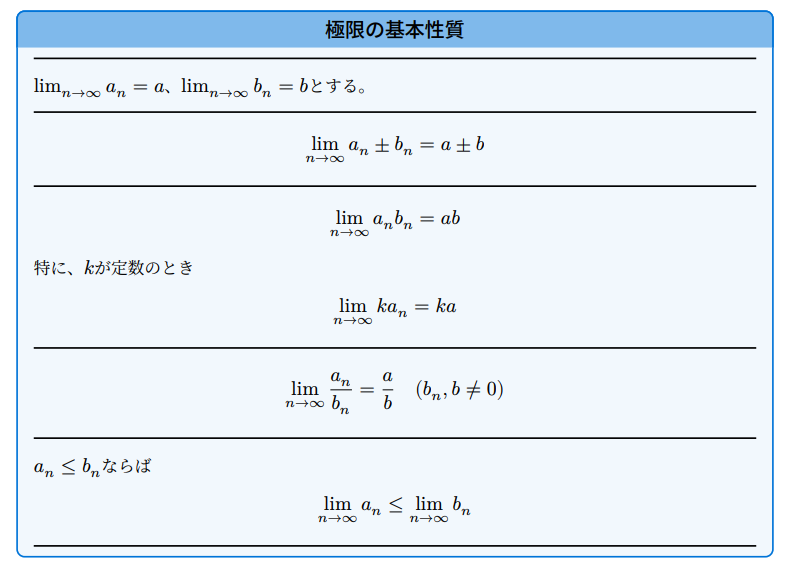
#line(length: 100%)は見やすさのために横線を入れているだけなので気にしないでください。

それでは記法に関する解説を行います。まず、Typstで数式を表記するためには$記号を用います。インライン数式は単に数式を$で囲むだけで表現できます。一方、ブロック数式は$の前後に空白をいれる必要があります。

Typstで極限を表記するにはlim関数を使用します。また、limに下付き文字として_(n->oo)のように指定することで、nが無限大に向かう極限であることを表せます。矢印はマイナス記号-と大なり記号>を組み合わせて->と表記します。また、無限大の記号はアルファベットのオーの小文字oを二つ並べてooと表記します。

プラスマイナス記号は、LaTeXでは\pmで表記しますが、Typstではplus.minusと表記します。ここはLaTeXに比べて少し面倒かもしれません。

分数を表記する際は単に/を用いて表記します。分母と分子を明確に指定するためには丸括弧()を用いるのが無難かもしれません。また、a/bを、関数fracを用いてfrac(a, b)と表記することもできます。

不等号を表す際は!=を使用します。また、不等号を表す際は<=や>=を使用します。このあたりの記法は、プログラミング言語のPythonなどの記法に近そうですね。この棒線つの不等号はgt.eqと表記しても同じように表示されます。また、棒線2つの不等号はgt.equivと表記することで表示されるようです。詳しくは公式ドキュメントのsymのページを参照してください。

合成関数の微分法

関数$y=f(x)$が区間$I$で微分可能、その値域$f(I)$で$z=g(y)$が微分可能ならば、\
合成関数$z=g(f(x))$は$I$で微分可能で、
  $ (dif z)/(dif x) = (dif z)/(dif y) (dif y)/(dif x) = g'(f(x)) f'(x) $

ライプニッツの記法を用いて微分を表す際は、difを用いて表記します。また、ラグランジュの記法を用いて微分を表す際に用いるプライム記号は単に'を用いて表記します。

基本的な関数の不定積分(抜粋)

$ integral e^x dif x = e^x $
#line(length: 100%)
$ integral a^x dif x = a^x / (log a) $
#line(length: 100%)
$ integral 1/x dif x = log |x| $
#line(length: 100%)
$ integral x^alpha dif x = x^(alpha+1) / (alpha+1) quad (alpha != -1) $
#line(length: 100%)
$ integral (dif x)/(sqrt(a^2-x^2)) = arcsin(x/a) $

インテグラル記号はintegralと表記して使用します。正直\int表記のほうがありがたいですが、もしかするとintキーワードが他の用途で使われているのかもしれません。ちなみにインテグラル記号はかなりの種類がサポートされているようです。

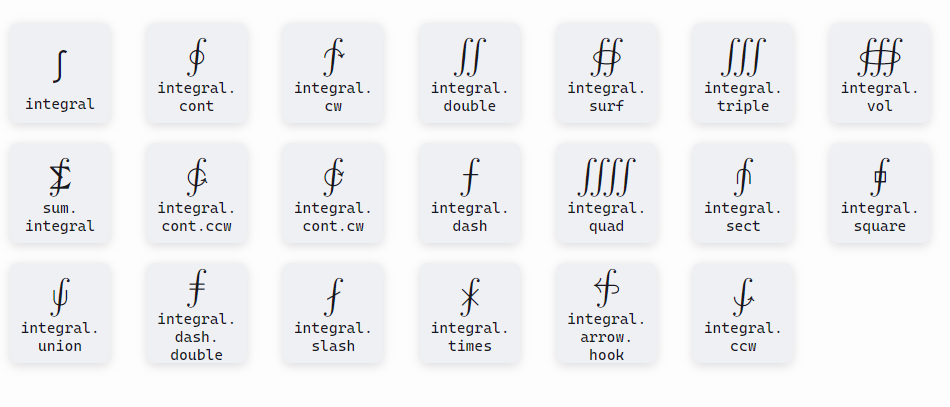
logの表記を行う際は普通にlogと表記します。また、絶対値記号を表す際は|か、あるいはabs関数を使用します。このあたりは直感的な記法なので問題ないと思います。

ギリシャ文字を用いる際は普通にalphaなどと表記すればよいです。今回は小文字を用いましたが、大文字を用いる際は頭文字を大文字にします。このあたりはLaTeXと同様ですね。また、LaTeXには例えばイプシロンには二種類の記号がありますが、Typstでもそのあたりはきちんとサポートされているようです(epsilonとepsilon.alt)。

平方根を用いる際はsqrt関数を使用します。また、平方根に限らず根号を使用する際はroot関数を使用します。詳しくはRootsのページを参照してください。

定積分の存在

$f(x)$が有界閉区間$[a, b]$上で連続であれば、
$ I = lim_(|Delta -> 0|) S(Delta) = lim_(|Delta -> 0|) sum_(i=1)^n f(xi_i)(x_i-x_(i-1)) $
 が存在する($I$は$[a,b]$の分割の仕方、$xi_i$のとり方によらない)。

総和記号を表す際はsum関数を使用します。また、総和記号の下限と上限を指定する際は、sum_(i=1)^nのように指定します。上限下限の指定の仕方はLaTeXと同じですね。定積分の区間の指定方法も同様です。

合成関数の微分

関数$z=f(x,y)$が全微分可能で、$x=phi(t), y=psi(t)$が$t$について微分可能ならば、合成関数$z=f(phi(t), psi(t))$は$t$について微分可能で、 次式が成り立つ。

$ (dif z)/(dif t) = (diff f)/(diff x) (dif x)/(dif t) + (diff f)/(diff y) (dif y)/(dif t) $

偏微分を表す記号はdiffあるいはpartialを用います。

ラグランジュの乗数法

$ cases(
  f_x(a,b) - lambda g_x(a,b) = 0,
  f_y(a,b) - lambda g_y(a,b) = 0,
  g(a,b) = 0
) $

連立方程式などを表記する際はcases関数を使用します。これを用いる際は、複数の式をカンマで区切って記述します。

線形代数学

行列の定義

$(m,n)$型の行列、$m times n$行列とは、$m times n$個の数の配列であり、記号で
$  mat(
  delim: "[",
  a_(11) , a_(12) , dots.h.c  , a_(1 n) ;
  a_(21) , a_(22) , dots.h.c  , a_(2 n) ;
  dots.v, dots.v, dots.down, dots.v ;
  a_(m 1) , a_(m 2) , dots.h.c , a_(m n);
)  $
と表される。$a_(i j)$を行列の$(i,j)$成分という。

掛け算の記号✕を表記する際はtimesを用います。また、行列を表記する際はmat関数を使用します。この関数を用いる際は、delimキーワードで括弧の種類を指定します。デフォルトでは丸括弧()ですが、今回は角括弧[]を指定しています。行列の要素を区切る際は行の区切りに;を、列の区切りに,を使用します。また、要素の省略を表すために、水平方向中央の点はdots.h.c、垂直方向の点はdots.v、右下方向の点はdots.downを使用します。

ベクトルの例

  $m$次元列ベクトル:
  $ bold(a) = vec(
    delim: "[",
    a_1,a_2,dots.v,a_m)
   $
  $n$次元行ベクトル:
  $ bold(b)=[b_1,b_2,dots.h.c,b_n] $
  零ベクトル: 成分がすべて$0$のベクトルで、記号で$bold(0)$と表す。

ベクトルなどを表す際に、アルファベットを太字表記するにはbold関数を使用します。

また、行ベクトルを表記する際はvec関数を使用します。こちらも、使用する括弧の種類はdelimで指定します。成分の区切り文字は,です。

列ベクトルを表記する際は特別な表記ではなく、[]などを使えば良さそうです。また、零ベクトルを表記する際はbold(0)と表記します。

ベクトル空間

  すべての$n$次元実数ベクトル$x$の集合を$n$次元ベクトル空間といい、記号で$bold(R)^n$と表す。\
  #line(length: 100%)
  スカラー倍に関する性質:
  $ bold(x) = [x_i] in bold(R)^n, a in bold(R) $
  のとき
  $ a bold(x) = [a x_i] in bold(R)^n $
  #line(length: 100%)
  和に関する性質:
  $ bold(x) = [x_i], bold(y) = [y_i] in bold(R)^n $
  のとき
  $ bold(x) + bold(y) = [x_i + y_i] in bold(R)^n $