第三章 電磁誘導方式

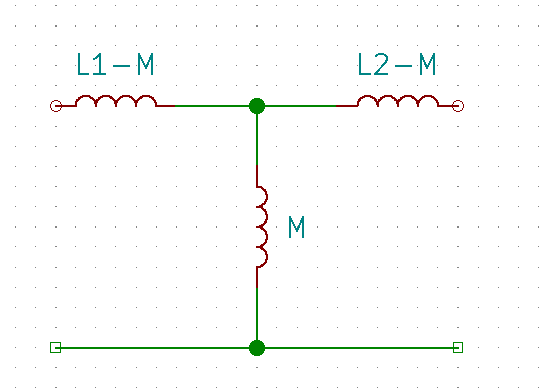
電磁誘導の等価回路を以下に示す。なお、送電コイル、受電コイルのインダクタンスをそれぞれL₁ 、 L₂とし、相互インダクタンスをMとしている。また、$M=k \sqrt{L_{1}L_{2}}$である。

等価回路から、結合係数kが大きいほど$$L_{1}-M$$や$$L_{2}-M$$での電圧降下が抑えられて負荷に大きな電圧を伝達することができる事がわかる。逆にkが小さいと電圧降下が大きく、負荷にまともに電圧を伝達することができないことは明らかだろう。またこのままでは誘導性であるため力率を改善するために一次側や二次側にキャパシタを挿入し、共振を利用する事が多い。このときの共振周波数はkに依存するため、距離依存性を持つ。とは言え、簡単に電力伝送を行うことができるためスマートフォンの無線充電などに応用がなされており、市場においても多数の商品を見ることができる（Qi規格など）。なお、効率は知らない。
個人で簡単に実験を行うのであれば、適当なハーフブリッジ回路、コイル２個、コンデンサがあれば良い。単純に一次コイルとキャパシタを共振させ、二次コイルを近づけると電力を取り出すことができる。ここで、受電コイルを遠ざけると二次電圧が減少するが、逆に近づけすぎても二次電圧が減少する。ファンクションジェネレータとオシロスコープを用意して見ると簡単に観測できるのだが、位置によって受電電力がピークを持つ周波数というのは変化する。つまり、ここに共振周波数の位置依存性を見ることができるのだ。
また、電力があまり取り出せないという場合にはコイルのQ値を見直すことをおすすめする。私の手元にある1W伝送（電源電圧9V時）が可能なコイルは直径50mmであり、Q値は100kHzで81.4である。共振周波数が低く、Q値が小さすぎる場合に伝送電力はほとんど取れなくなってしまう。色々周波数を変えて測定してみると面白いかもしれない。