岡山大学電子計算機研究会
取得に失敗しました

2018年度 入部

Twitter

2D

電子部品を燃やすのが得意

自己紹介

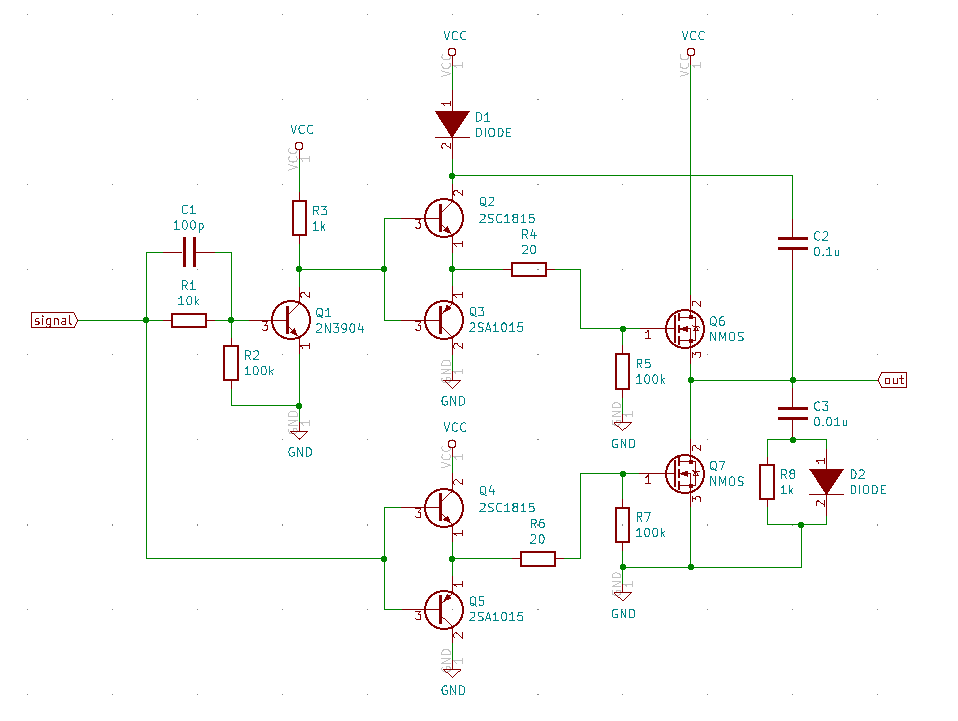
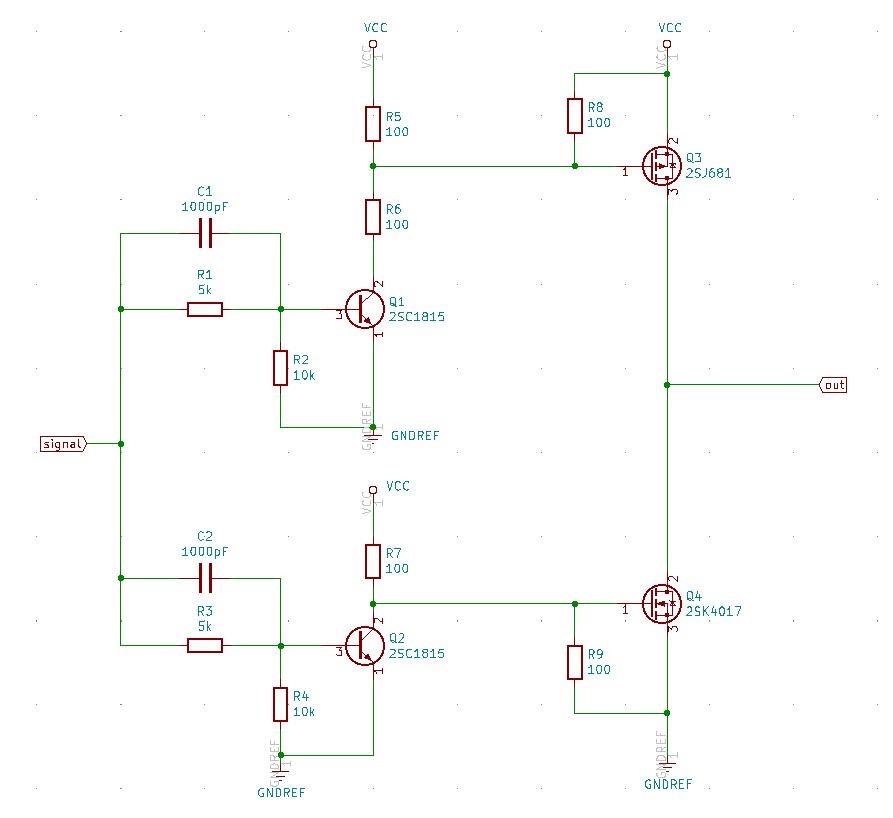
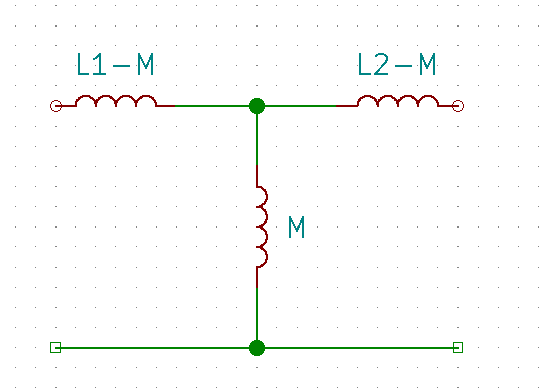
電子工作（主に無線電力伝送）と機械工作が趣味の電通4回生。
ワイヤレス給電システムの実験（電界結合も電磁誘導も）を個人で行っている。
それと、いろいろなものを壊すのが得意。下はほんの一例。
・ブレッドボード（900kHzでハーフブリッジ回路を駆動していたら燃えた）
・無線送電用コイル（端子台での固定が甘く、間隙で共振時に放電した）
・23インチモニター（うっかりUSBポートをショートさせてVGA入力が壊れた）
・Arduinoやセンサ類、各種トランジスタ（弾け飛んだり燃えたり）
・ハーフブリッジドライバIC（高温でブレッドボードが溶けた）

研究は電磁メタマテリアルと水中ワイヤレス給電をやっていくつもり。

自己紹介画像

取得に失敗しました

この人が書いた記事

記事「3Dプリンターで作るモッツァレラチーズ」のサムネイル Polygon

3Dプリンターで作るモッツァレラチーズ

※ちゃんとチーズを作ります。これを真似して何かあったとしても責任は取りません。 必要なもの 今回は3Dプリンタを用いてモッツァレラチーズを作っていきます。 早速ですが、必要な材料は以下の通りです。基本的にどこの家にでもあるものです。 低温殺菌牛乳（今回はタカナシ牛乳を使用）ボウル類穀物酢放射温度計（なければ接触式でも可）3Dプリンタ（ヒートベッドの最高温度が90度以上であること） 最悪、1,3,5さえあればOKです。温度は感じ取ってください。 牛乳は割引品を手に入れると割安です。1L300円以下ならチーズの既製品を買うより安くなります。 作り方を大雑把に言うと、牛乳を温めて酢を投入し、チーズを作ります。レンネットは使いません。 酢を投入してから50℃、30分の保温が必要らしいのですが、普通にやると温度管理が面倒です。 とはいえ、鍋につきっきりというのも面白くありません。 そこで、3Dプリンタのヒートベッドを恒温台として使用するわけです。 当然、面倒な温度管理は必要ありません。 作り方 さて、以下に過程を示します。 ヒートベッドで牛乳200mlを63℃付近まで温める穀物酢を10ml投入し、少しかき混ぜるこのまま50℃程度を維持しつつ、30分保温する析出物を漉す析出物を90℃の熱湯内に投入し、練り上げて完成 こちらが本調理の調理系です。実際にはこれに加えて放射温度計を取り付けています。 調理家電（3Dプリンタ）はENDER-2を使用しています。 電源は付属のものが怪しかったので自分で加工したジャンク品ATX電源を使用しています。 ヒートベッド温度は余裕を見て88℃としました（Control>Temperature>bed>88℃） 製造から完成まで それでは作っていきましょう。以下、写真が続きます。 あくまでも実験的調理ですから、数分ごとに温度を計測します。 結果はこの通り。縦軸はセルシウス温度（℃）、横軸は時間です。 Excelの関係上このように書いていますが、1790なら17時50分と読み替えてください。 ヒートベッドによる間接的加熱でも湯気が立つほどには昇温できます。 また、温度と時間は正の相関を持ちますが、ある値に向かって漸近する様子もわかります。 （実際、設定88℃だと牛乳は61℃付近で安定） さて、目標の63℃まで行きましたから酢を入れて軽く混ぜます。 あとはヒートベッド温度を70℃に設定して30分放置。 30分経ったのでザルに析出物を濾し取り、熱湯内で練って完成です。 素手で整形すると熱いですが、溶けたハンダよりは熱くないので何とかなります。 冷えた塩水に漬けて粗熱を取りつつ、塩味をつけましょう。 どうやらうまく行ったようです。 今回は200mlで作りましたから、製造原価は50円くらいですね。これでピンポン玉2つ分位できます。 市販のものが100gで300円程度なので、（少しは）買うより安いです。 ま、「自分でチーズ作ったんだぜ～！！」と自慢できるので、そのあたりを考えれば大幅なプラスですね。 「3Dプリンタで作ったんだぜ～！！」と言うと称賛と奇異の目で見られることは確実でしょう。 以上がモッツァレラチーズの作り方です。味は市販品と遜色無いものでした。 おまけ 最初は別メーカの低温殺菌牛乳を使用していました。しかし、酢の分量がまずかったのか、モッツァレラチーズではなくカッテージチーズに・・・。これはこれで美味しいです。

> 内容を見る

記事「SDカードの耐久試験レポート」のサムネイル Polygon
電子工作

SDカードの耐久試験レポート

※この記事で行ったことは真似をしないように！！！何かあっても責任は取りません！！！ ・・・ あらすじ 記憶媒体としてよく使うSDカード。HDDや磁気テープとは違い、これはフラッシュメモリを使用しているから磁気を近づけても問題はないらしい。 なんだかそう言われると、電気系としては限界を知りたいという気持ちが湧き上がってくる。 というわけで、どこまで無茶をするとダメなのかを知るためにも各種耐久試験を行ってみよう。 今回試験に用いるのは2GBのSDカード。確か初代3DSに付属してきたやつ。 ・・・ 定常磁界を印加してみる まずは定常磁界。これは単純にネオジム磁石でSDカードを挟むだけ。 一応、この磁石は公称値で磁束密度が260mTらしい。2600ガウスとも言える。 ここで、ふと昔に作った空芯コイルの存在を思い出したので、それも使ってみた。 結果は問題なし。普通に読み込めてしまった。 ・・・ 変動磁界を印加してみる 今度は変動磁界を印加して、誘起電圧による影響を見る。 変動磁界は適当に巻いたコイルを適当なコンデンサで共振させて発生させる。駆動回路は過去にも示したハーフブリッジ回路を使用した。 結果は問題なし。普通に読み込めてしまった。 ・・・ 冷凍してみる 今度はペルチェ素子とラジエーターを用いた水冷式冷却機で、一気にSDカードの温度を氷点下まで持っていく。ここで急激に温度を変化させるので、内部に結露とかが生じて何か影響が出るのかな？って予想。電気冷却だと冷凍庫とかじゃできないくらいの温度変化を起こせるのがポイント（数分で氷点下まで持っていける）。 結果は問題なし。氷の膜が張ったのにも関わらず、解凍すれば普通に読み込めてしまった。 ・・・ 変動電界に晒してみる 今度は変動電界にSDカードを晒す。ここで用いるのは少し前に自作した電界結合式ワイヤレス給電装置。極板間にSDカードを入れた状態で電力伝送を行う感じだけど、電界の影響は果たして・・・。 結果は問題なし。普通に読み込めてしまった。 ・・・ まとめ というわけで、なんとSDカードは無傷だった。頑丈過ぎやしないか・・・。 正直言って、コイルの上に置いたときに負荷電流が変化したから、こりゃ壊れたかなとか思ったが全然そんなことはなかった。というか、氷点下14度まで下げたのに普通に動いてるし。 もう、これを電気的に壊すには電子レンジに投げ込むしか無いんじゃないかなと思う。それか実験装置の大出力化（今で入力はMax10W）。 まあそういうわけで、よほどの環境に置かない限り電気的にはSDカードは破壊されないことがわかった。 というわけでSDカードの耐久レポートでした。 思ったよりも頑丈なことがわかったので、これからは物理的に破壊されない程度には雑に使っていこうと思う。 ちなみに、上記と同じことを磁気カードにやったら即データ消失すると思うから気をつけるように。

> 内容を見る

NoImage Polygon
電子工作

DAISOのLEDライトをパワーアップさせる

DAISOで売っているこのライト。 何か新歓のネタになるかなと思い、とりあえず一つ買ってきた。 見た感じ、砲弾型LEDが３つだけの構成。 パワーが足りないですよね？？？？？ そこで、早速ばらしてみた。リフレクタが有るからそのままでも十分明るいけどね～～。 少し悩んだけど、結局正面カバーを破砕して回路を取り出した。 一応、回路を上に押し上げると外せそうでは有るんだけども、面倒なので・・・。   見た感じ、チップ抵抗で電流を制限したLEDが3並列って構成？ LEDの並列接続はあまり良くないと思うけど、パワーLEDじゃないからいいのかな。チップ抵抗は何Ωだったのか不明。6R8に見えるけど、6.8Ωなわけないよな・・・。  ・・・  さて、早速改造していく。今回は裸の1WLEDを取り付ける予定。   まずはチップ抵抗と全てのLEDを取り外す。ハンダゴテで適当にやれば外れる。 次に電流制限抵抗を用意する。今回は順方向電圧3.2VくらいのLEDを使うので、電源を4.5Vとして残りの1.3Vで300mAくらい流れるようにすればいい。容量は1Wを最低とする（余裕を見て）ので、今回は10Ω0.5Wの3並列とした。これで等価的に3.3Ω1.5W。  ピークで390mAくらい流れてしまうけど、まぁいいや。そもそも、スペースが殆どない状況での改造だから無理があるのはご愛嬌。スペースがあれば定電流回路とか発振回路を入れたいところだけども。   早速用意した3.3Ω抵抗器をチップ抵抗の代わりに取り付ける。ショートしないように背面は絶縁しておくと安心。私は絶縁テープを敷いたけど、ぶっちゃけ何でも良いと思う。   あとは表面に1WLEDを取り付けて配線すれば完成。一応、LEDに熱伝導性の両面テープを貼り付けて基板にくっつけているけど意味はないと思う。放熱は考えない。   電気的な改造はこれで終わりなので、最初に破砕したパーツを3Dプリンタで印刷して組み上げ。 最後に、損失とか考えておこう。 抵抗では3.3Ωに1.3Vがかかるから、損失は約500mW。定格的にも大丈夫。 LEDは3.2Vで390mAだからピークで1.2W？・・・放熱がまずいなあ。                      ・・・   そこで、更に改造。 道具箱を漁ったら星型放熱板に取り付いたLEDを見つけたのでこれに換装する。電気的特性はほとんど同じ（電源で確かめた）だから、単に交換するだけでOK。 適度にハンダの煙を吸いつつ、うまいことはんだ付けして換装する。 ここで問題発生。なんと、放熱板の厚みが悪さをして正面カバーがはまらない。 そこで、リフレクターを廃棄して新しくスペーサ（直径23.4mmの円筒）を自前の3Dプリンタで印刷した。厚みは1mmだけど、力のかからない部分なので大丈夫。   これでパーツが揃ったので、さっと組み立てて今度こそ完成。 これにて終了。夜道を照らすくらいなら十分すぎる明るさになったと思う。 製作費用は本体代￥100円を含めて￥250くらいでした。

> 内容を見る

記事「ワイヤレス給電用　送受電コイル」のサムネイル Polygon
電子工作

ワイヤレス給電用　送受電コイル

Φ0.35mmのエナメル線を直径50mmの円状に10m巻いたもの（2.8Ω/350uH）。初期の頃に使用していたが銅損が大きく、効率も悪いので今は使用していない。

> 内容を見る

記事「ハーフブリッジ回路ができるまで　その6」のサムネイル Polygon
電子工作

ハーフブリッジ回路ができるまで　その6

６．後日談どうも最近知ったのだが、私のようにブレッドボードで数百kHzを出すのは異端らしい。確かに考えると、接触抵抗や寄生容量、浮遊インダクタンスの宝庫みたいなブレッドボードで500kHzなんて周波数を扱うのはまずい。というか、原因不明のトランジスタ爆発や回路の焼損はこの寄生容量やインダクタンスによるものな気がする。今後は気をつけよう。７．ギャラリー最終型の回路図

> 内容を見る

記事「ハーフブリッジ回路ができるまで　その5」のサムネイル Polygon
電子工作

ハーフブリッジ回路ができるまで　その5

５．スナバ回路＆ブートストラップ回路の導入（～2MHz）ハイサイドのPchをNchに交換することにした。そこで生じるゲート電位の不都合※はブートストラップ回路で解決する。しかし、このときの回路ではノイズが激しく、電源電圧を9V以上にすると異常発振を起こして回路が燃えてしまう事がわかった。そこでスナバ回路を導入し、サージ電圧を低減するようにした。このスナバ回路の効果は素晴らしく、電源電圧を最大20Vまで引き上げることに成功し、動作速度では最大2MHzにも達した（数百mA以上を流す場合は500kHzまでだが・・・）。スナバ回路はRCD型を採用したが消費電流は10mA以下と、安定して動作してくれている。現在はこの回路が最新。 ※Nchはゲート電位がソース電位に対して高い場合（しきい値電圧次第）にONする。しかし、ハイサイドをNchにしてしまうとソース電位が電源電圧と同じ電位になってしまい、ハイサイドをONするには電源電圧以上の電圧が必要となってしまう。一般に、回路内での最大電圧は電源電圧であるためこれでは不都合が生じる。   なお、スナバ回路の素子定数は実験的に決定したため、理論的な計算は行っていない。

> 内容を見る

記事「ハーフブリッジ回路ができるまで　その4」のサムネイル Polygon
電子工作

ハーフブリッジ回路ができるまで　その4

４．停滞期（発振回路で遊ぶ）ゲート電位の問題を解決できなかったので、Pchが吹っ飛ばないように祈りながら回路を使っていた。また、この頃からパワーLEDで遊ぶようになり、オペアンプで発振回路を組んだり、トランジスタで定電流回路を組んでいた。特に矩形波発振回路は面白く、理論式の導出も行った（使用していたオペアンプだとスルーレートに制限され、100kHz程度で発振が限界を迎えるのだが）。なお、この回路はかいわれ大根栽培装置に応用されている。

> 内容を見る

記事「ハーフブリッジ回路ができるまで　その3」のサムネイル Polygon
電子工作

ハーフブリッジ回路ができるまで　その3

３．SEPP回路の導入（～500kHz）この頃から、どうもコレクタ負荷から信号を取り出してFETを駆動するのは遅いと勘付き始めていた。そこでSEPP（Single Ended Push-Pull）回路を導入してFETのゲート容量を高速に充放電することにした。また、それに加えてFETの寄生容量とゲート抵抗による過渡現象も考慮して回路を改修した。それが以下の写真である。 結果は大成功。ついに500kHzの壁を突破し、目標を達成した。ここからしばらくはこの回路でワイヤレス給電の実験を行うことになる。とはいえ、この回路は時々ハイサイドのPchMOSFETが吹っ飛ぶという欠陥を抱えていた。オシロスコープで各FETのゲート電位を見ると、特にハイサイドのPchでしきい値ギリギリの弱々しい波形が見えた。これでは動作はしても大電流を負荷に供給することができない（これが高周波域で負荷を接続すると大きな電圧降下が起きる原因だと思われる）。更に、ハイサイドがPchMOSFETだから高速化に限界が見え隠れしている。まだまだ改善が必要だ。

> 内容を見る

記事「ハーフブリッジ回路ができるまで　その2」のサムネイル Polygon
電子工作

ハーフブリッジ回路ができるまで　その2

２．ディスクリート化（～300kHz）市販のICでは高速化に限界があると思い、ディスクリート部品でハーフブリッジ回路を組むことに。この頃はSEPPなどを知らなかったものだから、エミッタ接地のC1815トランジスタに付けたコレクタ負荷から信号を取り出してFETを駆動させていた。 こんなものでも100kHzの壁を超えることができた。とはいえ、単にトランジスタに100kHz以上の信号を入れるだけでは動作しない。これは少数キャリアの蓄積効果によるものであり、C1815なら大体1kHz以上で動作しなくなる。解決策は簡単で、ダンパ抵抗に並列にpFのコンデンサを入れるだけ。これをスピードアップコンデンサと言い、信号の立ち上がり時には瞬間的にCのインピーダンスが0になり、高速にベースへ電荷を注入できる。また、立ち下がり時にはCによってベース電位が負となり、高速に電荷を引き抜くことができる。容量はごく小さなもので良いのだが、私は何故か1000pFを入れていた。   しかし、依然として500kHzには届かない。まだまだ改善が必要だ。

> 内容を見る

NoImage Polygon
電子工作

ハーフブリッジ回路ができるまで　その1

０．あらましワイヤレス給電を実験するにあたって、矩形波電源が必要になった。軽く調べてみると、どうもハーフブリッジ回路がメジャーらしい。そこで、ハーフブリッジ回路を作成することにした。試行錯誤するのは目に見えているのでブレッドボードを用意し、機動的に回路を変更できるようにした。最終的に500kHzで動作するハーフブリッジ回路を構築することに成功した（軽負荷なら2MHzでも動作可能）が、一先ずワイヤレス給電の実験が終了したのでそれ以上は踏み込んでいない。１．ドライバICの導入（～100kHz）まだまだ電子工作を知らなかった時代。ハーフブリッジドライバ「IRS2108」を使用し、FETをドライバICで駆動していた。しかし、このICはデッドタイムが自動で540ns入る関係かどうかわからないが、100kHz以上での動作が困難だった。   まだまだ改善が必要だ。

> 内容を見る

NoImage Polygon
電子工作

無線給電　補章

補章　結合係数の導出結合係数kの測定方法として、相互インダクタンスMからの導出法がある。 それでは、実際に導出を行っていこう。   一次側コイルと抵抗をつないだ回路に電源$$E_{1}=E \sin \omega t$$を接続したとする。 すると回路方程式はフェーザを用いて以下のようになることは明白だろう。   $$\dot I = \frac{\dot E}{\dot Z}=\frac{E}{\sqrt{2}\sqrt{R^{2}+(\omega L_{1})^{2}}}e^{-j\phi}$$  ここで、 φはインピーダンス偏角であるので、以下の通り。   $$\phi=\tan^{-1}(\frac{\omega L_{1}}{R})$$  つまり、i1は瞬時値を考えて以下を得る。   $$i_{1}=\sqrt{2}IM(\dot I e^{j\omega t})=\frac{E}{\sqrt{R^{2}+(\omega L_{1})^{2}}}\sin(\omega t-\phi)$$    二次側は開放しているので相互インダクタンスの影響しか現れないことを考えると、二次側電圧 は以下を得る。この際、二次側に電流が流れないのでコイルの抵抗による電圧降下は無視できることに注意したい。   $$v=M\frac{di_{1}}{dt}=M\frac{d}{dt}{\frac{E}{\sqrt{R^{2}+(\omega L_{1})^{2}}}\sin(\omega t-\phi)}$$  すなわち、                                                                                $$v=\frac{\omega ME}{\sqrt{R^{2}+(\omega L_{1})^{2}}}\cos(\omega t-\phi)$$      これで二次側電圧と相互インダクタンスの関係式が導かれた。 二次側電圧vのピーク電圧をvmaxとすると以下のように三角関数成分を消すことができる。   $$v_{max}=\frac{\omega ME}{\sqrt{R^{2}+(\omega L_{1})^{2}}}$$  それではMの式を導こう。先に示した式を変形して以下を得る。   $$M=\frac{\sqrt{R^{2}+(\omega L_{1})^{2}}}{\omega E}v_{max}=\frac{\sqrt{R^{2}+(2\pi fL_{1})^{2}}}{2\pi fE}v_{max}$$  つまり、結合係数kは以下で求めることができる。   $$k=\frac{M}{\sqrt{L_{1}L_{2}}}=\frac{\sqrt{R^{2}+(2\pi fL_{1})^{2}}}{2\pi fE\sqrt{L_{1}L_{2}}}v_{max}=\frac{\sqrt{R^{2}+(2\pi fL)^{2}}}{2\pi fEL}v_{max}$$  ここからはさらに変形を行っていこう。まずはωを含む式にkを変形する。   $$k=\frac{\sqrt{R^{2}+(\omega L)^{2}}}{\omega EL}v_{max}$$  ωL＝RQであることを考えて以下を得る。（Q値の導出を参考）   $$k=\frac{\sqrt{R^{2}+(RQ)^{2}}}{RQE}v_{max}=\sqrt{\frac{R^{2}(1+Q^{2})}{(RQE)^{2}}}v_{max}=\frac{\sqrt{1+Q^{2}}}{QE}v_{max}$$  ここで、Q>>1であるならばQ>０より以下を得る。   $$k=\frac{\sqrt{Q^{2}}}{QE}v_{max}=\frac{v_{max}}{E}$$  すなわち、Q>>1であるならば結合係数は近似的に入出力ピーク電圧の比で与えられる。

> 内容を見る

記事「無線給電　第四章」のサムネイル Polygon
電子工作

無線給電　第四章

第四章　電界結合方式電界結合の等価回路を以下に示す。なお、電極間で形成されるキャパシタンスをそれぞれC1、C2 （一般に$C_{1}=C_{2}$）、相互キャパシタンスをCmとしている。 図から、C1-Cm（C2-Cm）は漏れキャパシタンスとみなすことができる。また、相互キャパシタンスCmが大きいほど二次側に電圧を伝達しやすく成り、大きな電力を伝送することができることがわかる。相互キャパシタンスは電極面積を大きくしたり、電極間距離を小さくすることで改善することが可能であるが、どれも現実的にはある程度の制約が存在する。また、電極間に形成される容量は極めて小さな値である（試作電極板で200pF以下）から、これを超えて電力伝送するには大きな電圧や高い周波数が必要となる。 これを解決するために直列にインダクタを入れて共振させる方法（直列共振法）や、並列にキャパシタやトランスを入れることにより外部回路で共振系を構成する方法（並列共振法）などもあるが、電界結合方式自体が電磁誘導方式に対してマイナーであるため先行事例が少ない。故に、個人で電界結合を用いてワイヤレス給電を行ったという記録もほとんど確認されない（電磁誘導方式ならいくつも見つかるのだが）。しかし、1W程度なら個人実験レベルでも簡単に伝送することができる。図に示すのは私が実際に構築した電界結合方式の無線送電システムである。電極は中央に写っている200mm×100mm×5.5mmのMDFに貼り付けた銅箔であり、電極に限って言えば極めて軽量、低発熱である。 スペックを簡単に示す。   ・電源電圧　12V ・送電電力　1W（二次側負荷100Ω時） ・周波数　580kHz ・効率　30％（DC to AC） ・最大伝送距離　6mm   高周波トランスは自作したものであるから、効率は更に向上させることができると考えられる。1W伝送時の負荷は100Ω抵抗であったが、図の通り負荷としてRE-280モータをつないでも十分に動作する（この場合はFRDで半波整流して適当な平滑コンデンサを接続した）。これを見ても分かる通り、電界結合方式というのは案外簡単に実現できるのだ。しかし、効率や手軽さ、システムの大きさといった点では電磁誘導方式に負けているため、まだまだ改善が必要である。なお、次の目標は水中での1W伝送である。

> 内容を見る

記事「無線給電　第三章」のサムネイル Polygon
電子工作

無線給電　第三章

第三章 電磁誘導方式電磁誘導の等価回路を以下に示す。なお、送電コイル、受電コイルのインダクタンスをそれぞれL1 、 L2とし、相互インダクタンスをMとしている。また、$M=k \sqrt{L_{1}L_{2}}$である。 等価回路から、結合係数kが大きいほど$$L_{1}-M$$や$$L_{2}-M$$での電圧降下が抑えられて負荷に大きな電圧を伝達することができる事がわかる。逆にkが小さいと電圧降下が大きく、負荷にまともに電圧を伝達することができないことは明らかだろう。またこのままでは誘導性であるため力率を改善するために一次側や二次側にキャパシタを挿入し、共振を利用する事が多い。このときの共振周波数はkに依存するため、距離依存性を持つ。とは言え、簡単に電力伝送を行うことができるためスマートフォンの無線充電などに応用がなされており、市場においても多数の商品を見ることができる（Qi規格など）。なお、効率は知らない。 個人で簡単に実験を行うのであれば、適当なハーフブリッジ回路、コイル２個、コンデンサがあれば良い。単純に一次コイルとキャパシタを共振させ、二次コイルを近づけると電力を取り出すことができる。ここで、受電コイルを遠ざけると二次電圧が減少するが、逆に近づけすぎても二次電圧が減少する。ファンクションジェネレータとオシロスコープを用意して見ると簡単に観測できるのだが、位置によって受電電力がピークを持つ周波数というのは変化する。つまり、ここに共振周波数の位置依存性を見ることができるのだ。 また、電力があまり取り出せないという場合にはコイルのQ値を見直すことをおすすめする。私の手元にある1W伝送（電源電圧9V時）が可能なコイルは直径50mmであり、Q値は100kHzで81.4である。共振周波数が低く、Q値が小さすぎる場合に伝送電力はほとんど取れなくなってしまう。色々周波数を変えて測定してみると面白いかもしれない。

> 内容を見る

NoImage Polygon
電子工作

無線給電　第二章

第二章　電界vs磁界現在実用化されている無線送電は主に電磁誘導方式と電界結合方式の２つである（他にはマイクロ波送電方式や超音波伝送方式も有るが、メジャーとは言い難い）。つまり、無線送電は電界と磁界のどちらかを伝送手段として用いる事が多いのだ。電磁誘導方式と電界結合はどちらにもメリットがあり、優劣付け難いものである。しかし、実用化という観点からすれば電磁誘導方式が圧倒的に優勢である。これはある程度の電力を簡単に送電できるという電磁誘導方式特有の手軽さが大きいと思われる。 電磁誘導方式は極端に言えば割れたトランスである。送電コイルと受電コイルを磁気的に結合させ、磁界を用いて電力伝送を行う。そのため、コイルに流れる電流が重要となる。また、コイル単体では誘導性負荷となってしまうのでコイルに共振コンデンサを接続し、共振を利用して力率を改善する事が多い。更に、Q値が高くなければ多くの電力を入力できないため、低損失なコイルを高い共振周波数で駆動することが鍵となる。しかし、この共振周波数は結合係数に依存するので位置によって伝送電力が変化してしまうという大きな問題点を抱える（ロバスト性が悪い）。これを如何に解決するかが電磁誘導方式の課題である。 電界結合方式は極端に言えばキャパシタである。水平方向のロバスト性が高く、ズレに強い方式であると言える。この方式は対向電極間に生じる容量（等価的なキャパシタ）を経由して負荷に電力を伝送する方式であり、電力伝送は電界によって行われるので、電圧が重要となる。また、高電圧で電力伝送するので流れる電流は小さく、電極での発熱が殆どない。しかし、地上では空気コンデンサそのものであるので容量が極めて小さく、周波数や電圧が低いとそのインピーダンスによって電力伝送をまともに行えない。仮に共振を利用しても電極間距離で容量が劇的に変化してしまうので、電磁誘導方式と同様の問題点を抱える。 つまりまとめると、電磁誘導方式はコイルの発熱と重量が問題となり、重量が問題となる宇宙空間では適用が難しい。しかし回路構成は簡単であり、地上に限れば有力な電力伝送手段である。電界結合方式はその性質上高電圧を用いるため感電の危険性や空中放電の可能性があり、地上では適用が難しい。しかし電極は金属箔などでも良いため極めて軽量であり、発熱をほとんど生じないため宇宙などでの適用が考えられる。なお、両者に共通する問題点として、受電側の位置や負荷によって送電電力が変化してしまい、場合によっては全く送電できなくなってしまうというものが有る。なお、水中では電磁誘導方式と電界結合方式の両方が検討、研究されており、手軽さや送電可能電力という面で見れば電磁誘導が、システム重量といった面で見れば電界結合が有利となる。

> 内容を見る

NoImage Polygon
電子工作

無線給電　第一章

第一章　序論近年、「置くだけ充電」や「Qi」という言葉を聞くことが多くなってきたと思う。これらは無線給電技術の最たる例であり、主に共振現象を応用して実現されている。意外に思われるかもしれないが、無線給電自体は簡単に実験で確認することのできるものであり、電気、特にエネルギー伝送に興味がある者なら一度はその構築を目指すだろう。そこで僭越ながら、電気初学者ではあるが私が各素子や電気特有の概念などを説明しつつ、無線給電回路の紹介を行いたいと思う。この稚拙な記事を読んで、少しでも電気に興味を持ってくれたら電気を専攻するものとしてこの上ない喜びである。また、電気初学者故、理解の甘い部分や間違いなどが多少はあるかと思う。そこはどうか容赦願いたい。

> 内容を見る

岡山大学電子計算機研究会
© 2023 OUCRC All rights reserved